[AI] 회귀분석 개념

둘 이상의 변수 간의 관계를 보여주는 통계적 방법. 일반적으로 그래프로 표현되며 종속 변수와 독립 변수 간의 관계를 테스트한다.

회귀 분석의 시나리오 예시:

1) 가상의 소매 기업이 다음 달(또는 종속 변수)의 판매 수치를 예측하고자 함.

2) 날씨, 새 모델 출시, 경쟁업체가 수행하는 작업 또는 외부 포장 도로에서 진행 중인 유지 관리 작업(독립변수) 등을 고려

3) 회귀 분석을 통해 측정 가능한 모든 변수를 정렬, 어떤 변수가 영향을 미칠 것인지 논리적으로 분석

4) 분석을 통해 판매에 영향을 미치는 요인과 변수가 서로 상호 작용하는 방식 산출

5) 기업의 의사결정에 반영

→ 종속 변수 : 판매, 독립 변수: 날씨, 경쟁사 행동, 보도 유지 관리 및 새 모델 출시

머신러닝에서 가장 일반적인 회귀분석 유형이라고 할 수 있는 선형 회귀는 예측 변수와 종속 변수로 구성되며, 이 둘은 선형 방식으로 서로 연관지어져 있다. 선형 회귀는 위에서 설명한 대로 가장 적합한 선, 즉 최적적합선을 사용한다.

변수들이 서로 선형적으로 연결되어 있는 경우 선형 회귀를 사용한다. 광고 지출 증가가 판매에 미치는 영향을 예측할 때 등이 예가 될 수 있다. 그러나 선형 회귀분석은 특이치에 영향을 받기 쉬우므로 빅데이터 집합을 분석하는 데 사용해서는 안 된다.

트레이닝 데이터를 분석하고 데이터의 분포를 가장 잘 나타내는(오차가 최소인) 일차함수의 기울기(가중치) W, y절편 b(bias)를 찾는 과정 → y = Wx + b

Loss/Cost Function (손실 함수)
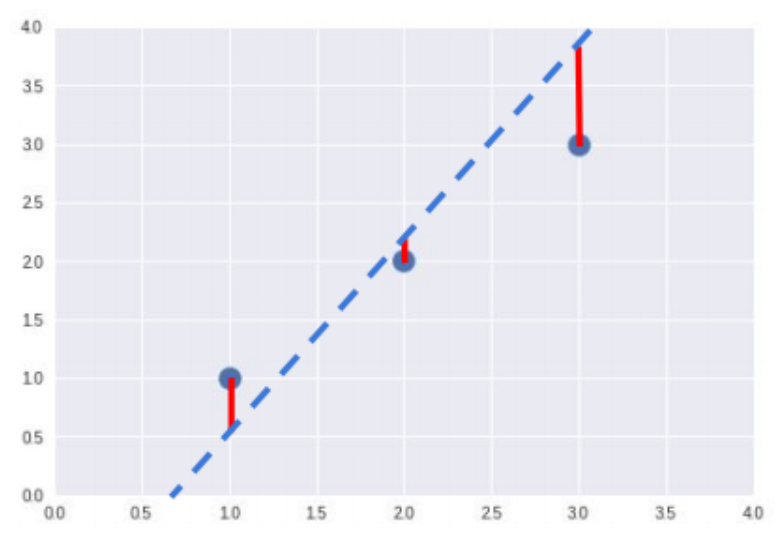
손실함수의 목적 : 빨간선(평균값과 예측값의 차이)의 총합을 최소화 하여 최적의 결괏값을 도출 하는 것
손실 함수는 데이터를 토대로 산출한 모델의 예측 값과 실체 값과의 차이를 표현하는 지표로, 모델 성능의 ‘나쁨’을 나타낸다. 어떤 방식으로 표현하느냐에 따라 여러가지 손실 함수가 존재 ex) 회귀 타입 : MAE,MSE,RMSE , 분류 타입 : Binary cross-entropy , Categorical cross-entropy

#### MSE(Mean Square Error)